Scripts for Step 1 - Prepare the continuum:

Initial Self-Calibration#

In preparation for the phase alignment, we do a single round of self-calibration on each execution block. (With all SPWs combined; we’re not at the per-SPW stage yet). Since the outcome of the phase alignment step all depends on the visibility phases, the idea is that this initial round of self-cal will help get the phases in good shape.

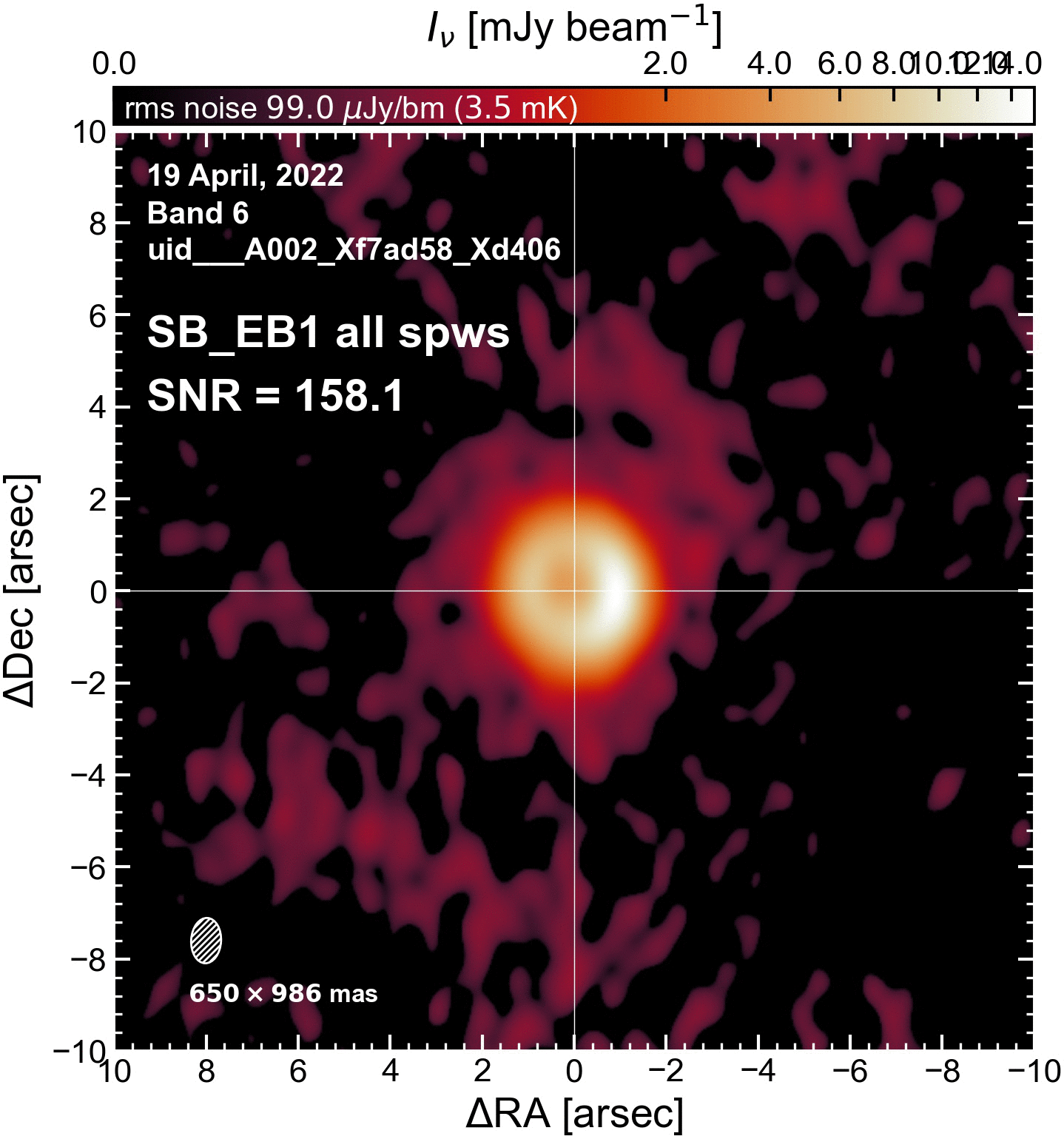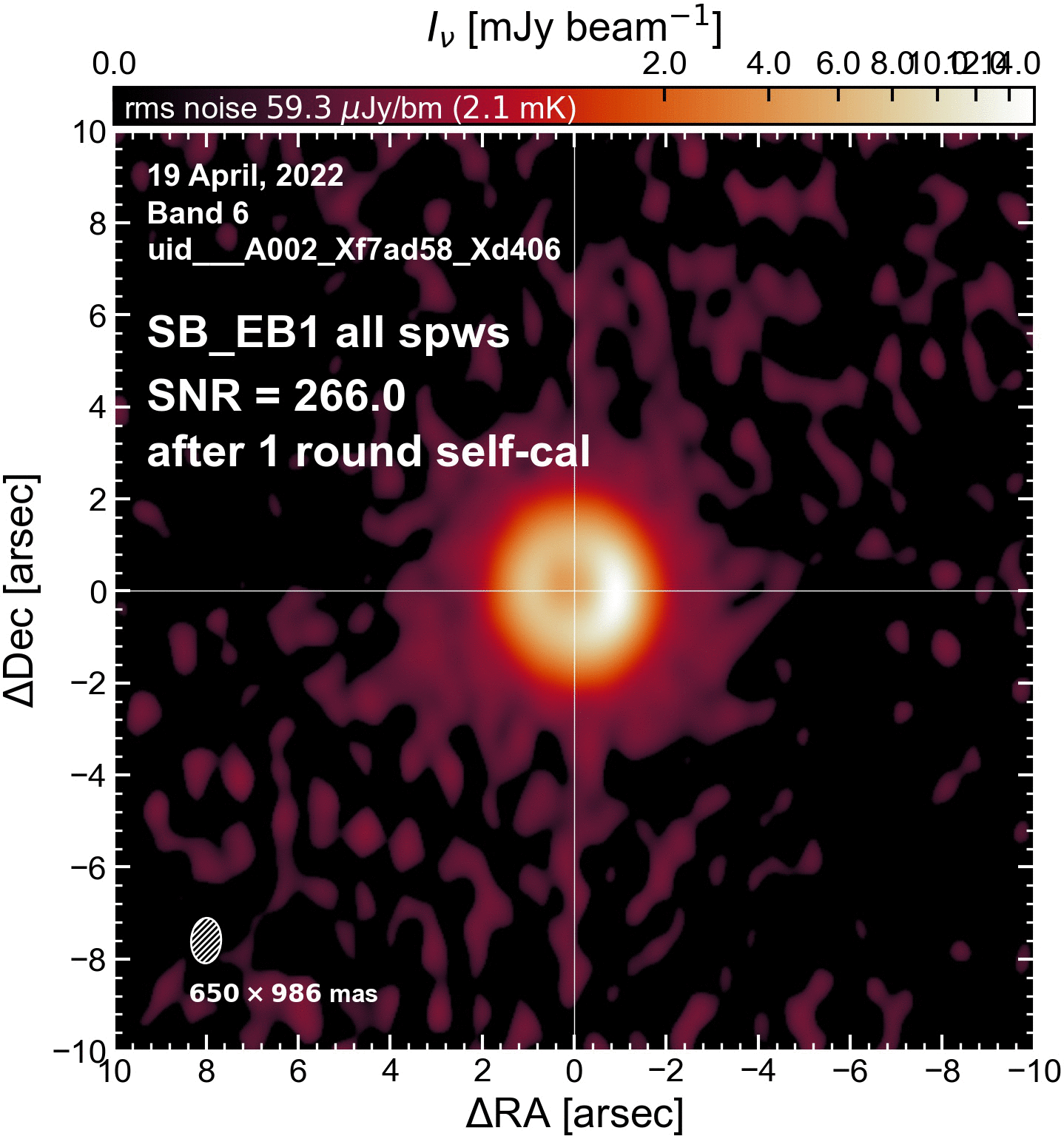
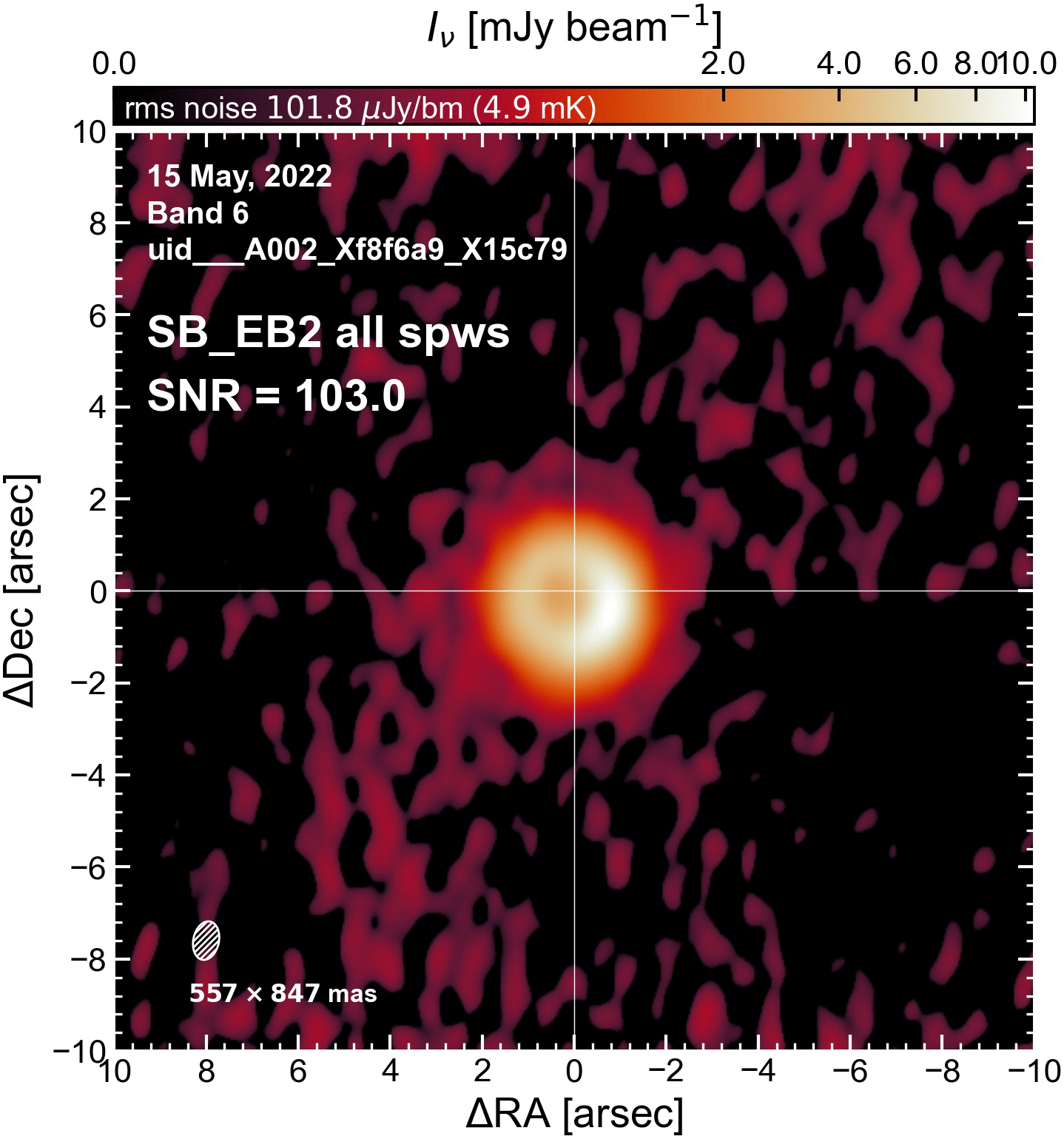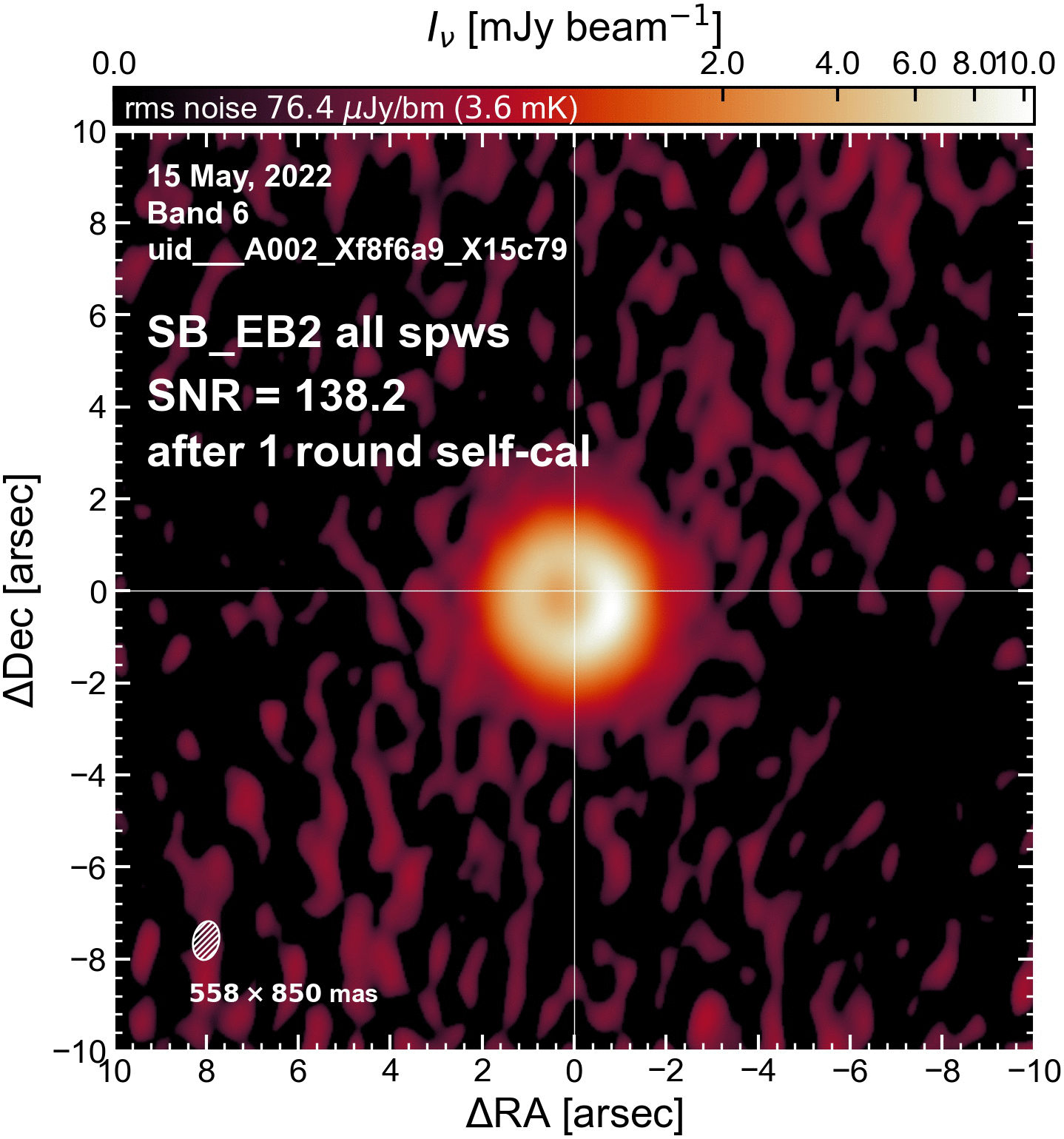
Initial model: The first step of self-cal is to generate an initial model. For each EB we make a new clean image, cleaned very shallowly and interactively. These are different from the initial continuum images from the previous page, and they don’t look as good because they are not cleaned as deeply. What matters here is that we trust the MS table column 'MODEL' phases; the amplitudes are not important at this stage.

Initial model alternatives

What should you take as the initial model?

There are many options, and which one is most appropriate depends entirely on your source. Here’s some options I’ve heard of:

  • A shallowly cleaned image (as we do here)

  • A model made from analytic fit to the visibilities (if possible)

  • An axisymmetric model (if there’s good reason), e.g. an azimuthal average of a shallowly cleaned image

It’s hard/impossible to tell a priori what is the right choice (except in the case of a point source!). This is a significant consideration and a deep topic. What you put in greatly influences what you get out.

Deconvolution: This sounds like a detail but it is not. The model will be comprised of clean components, which will be a collection of functions of your choice. We choose \(\delta\)-function clean components, i.e. Hogbom deconvolution. An alternative choice may be 'multi-scale' clean, in which case the model basis functions would be Gaussians. The current wisdom is that Gaussians don’t make a great basis for concentric ring structures like we expect in continuum images of disks (including AB Aur).

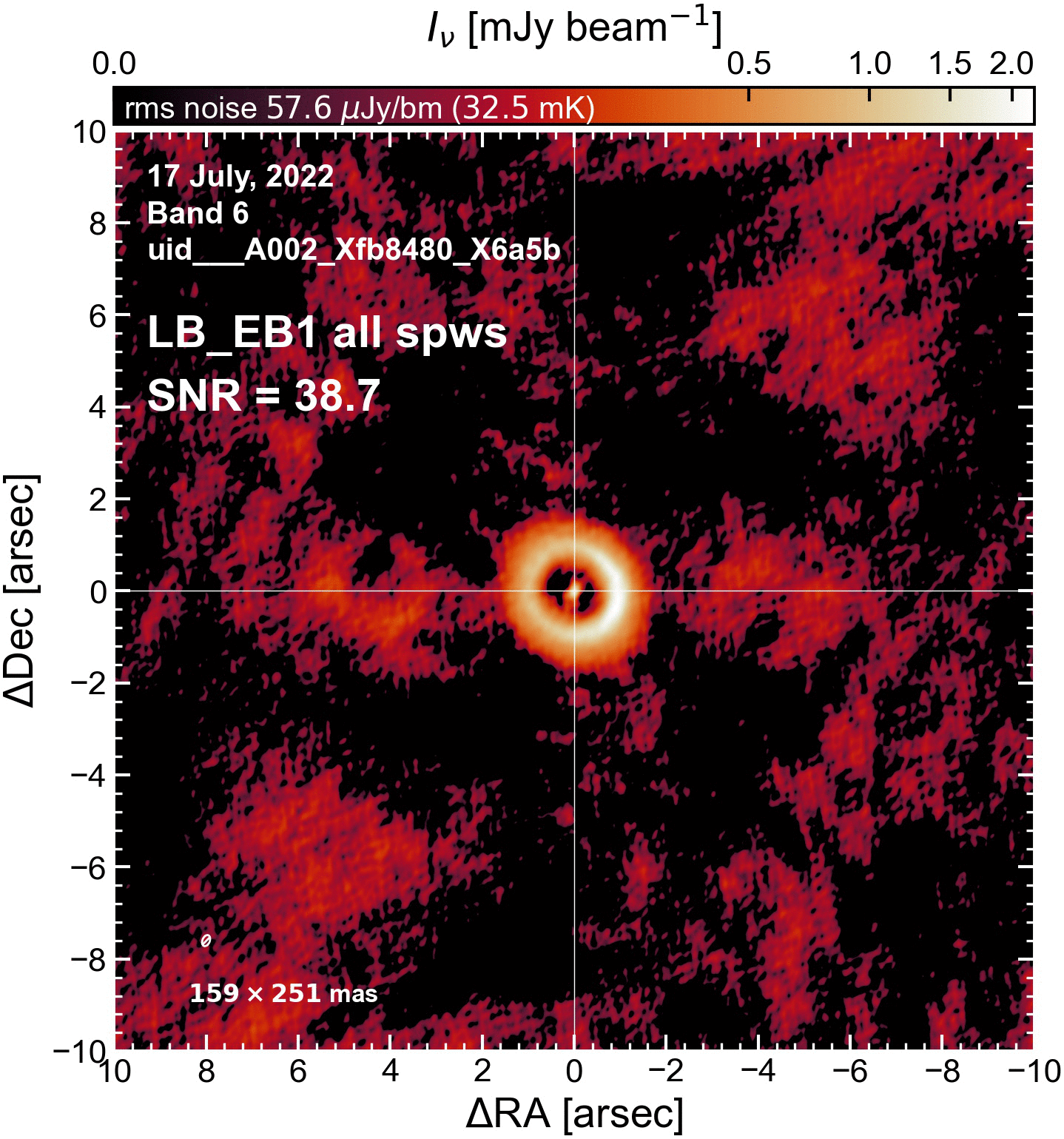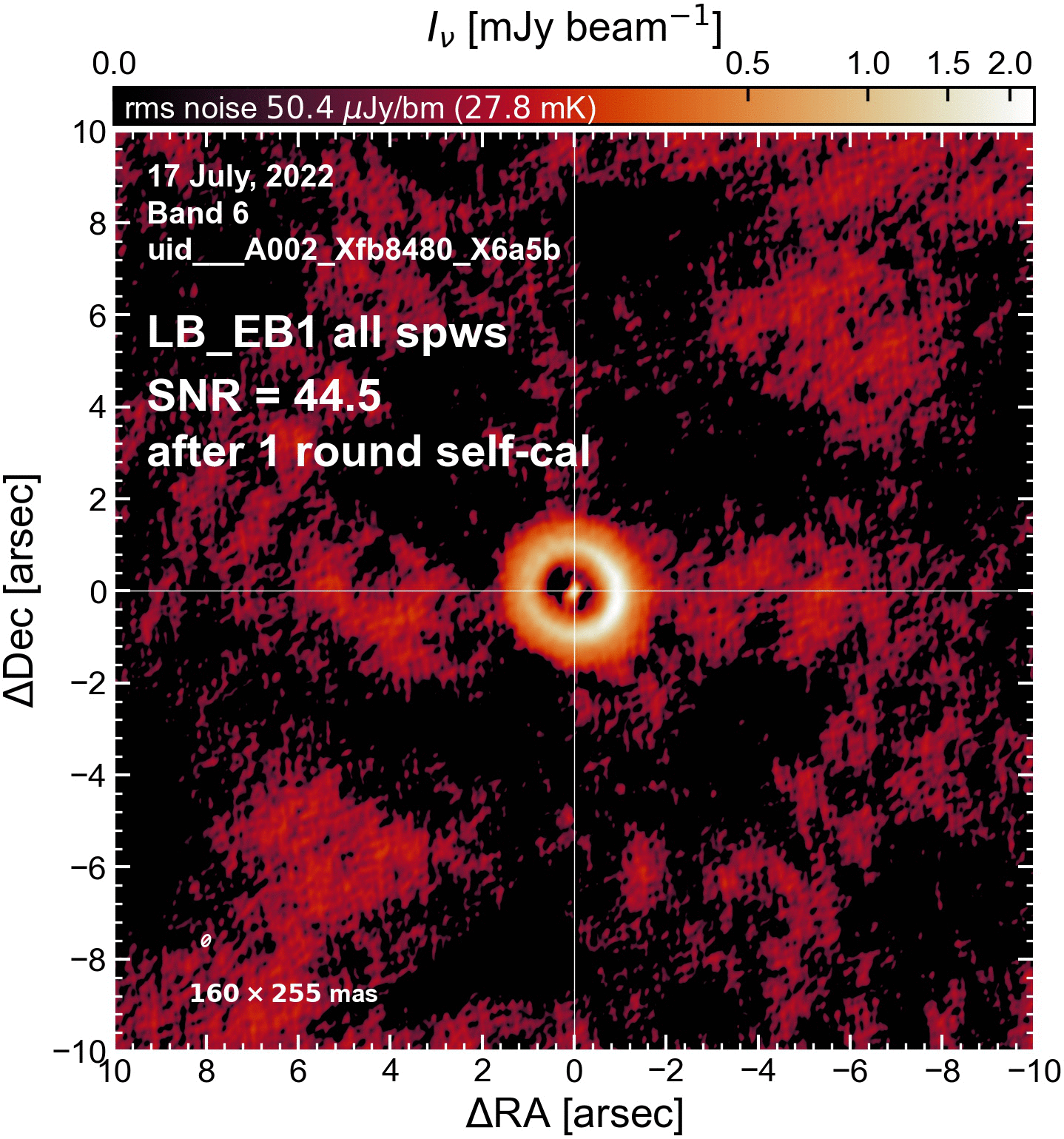
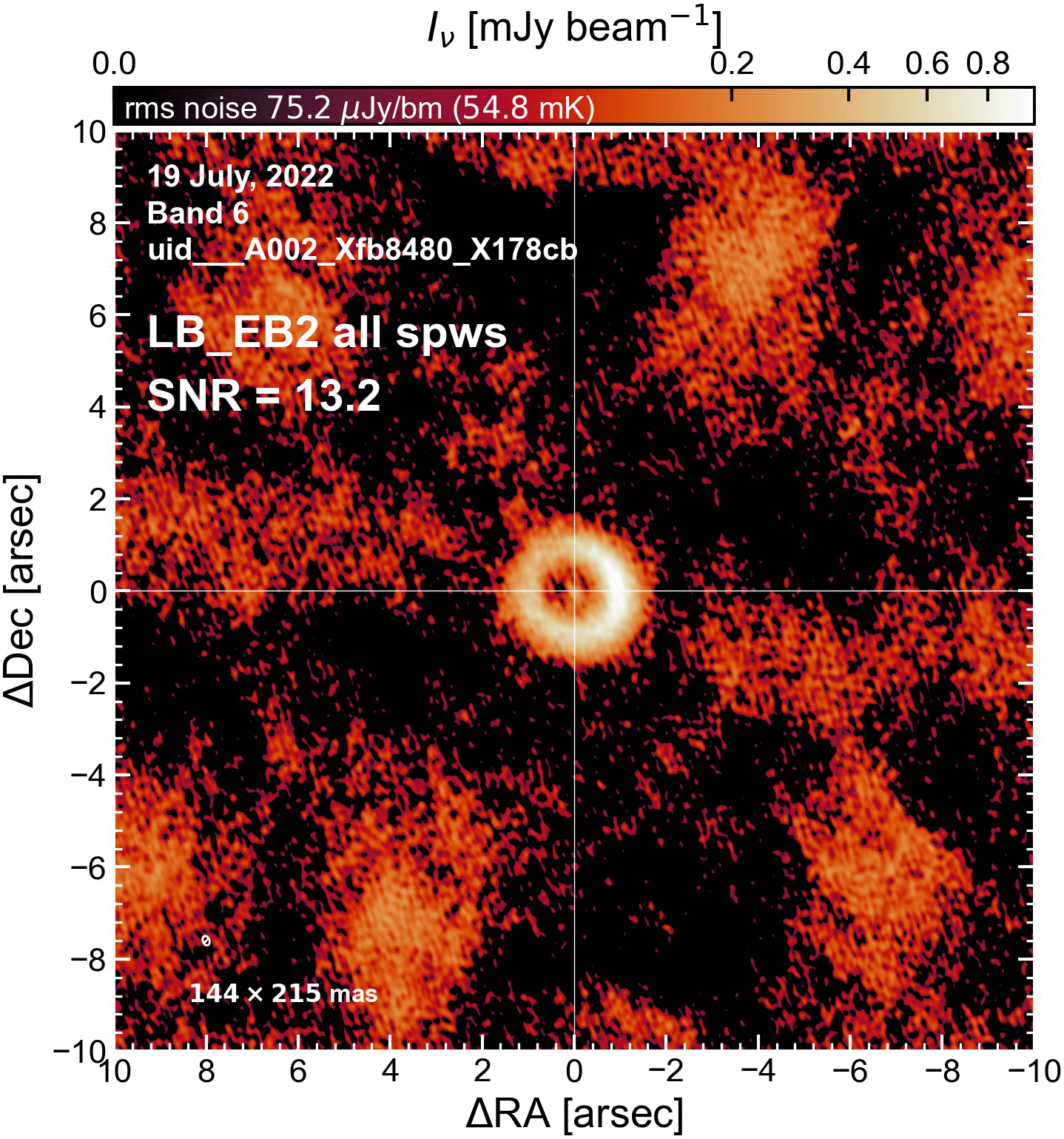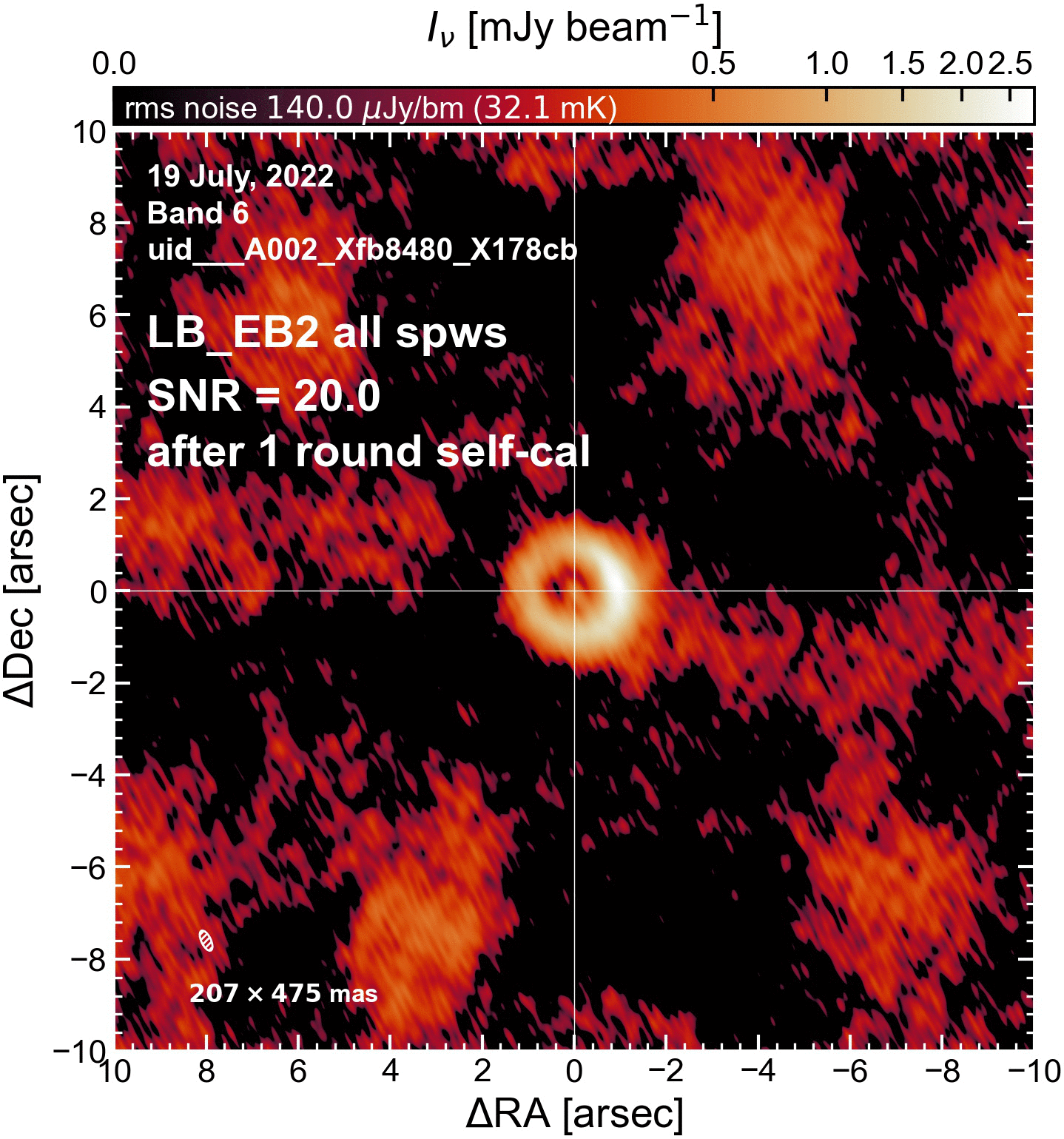
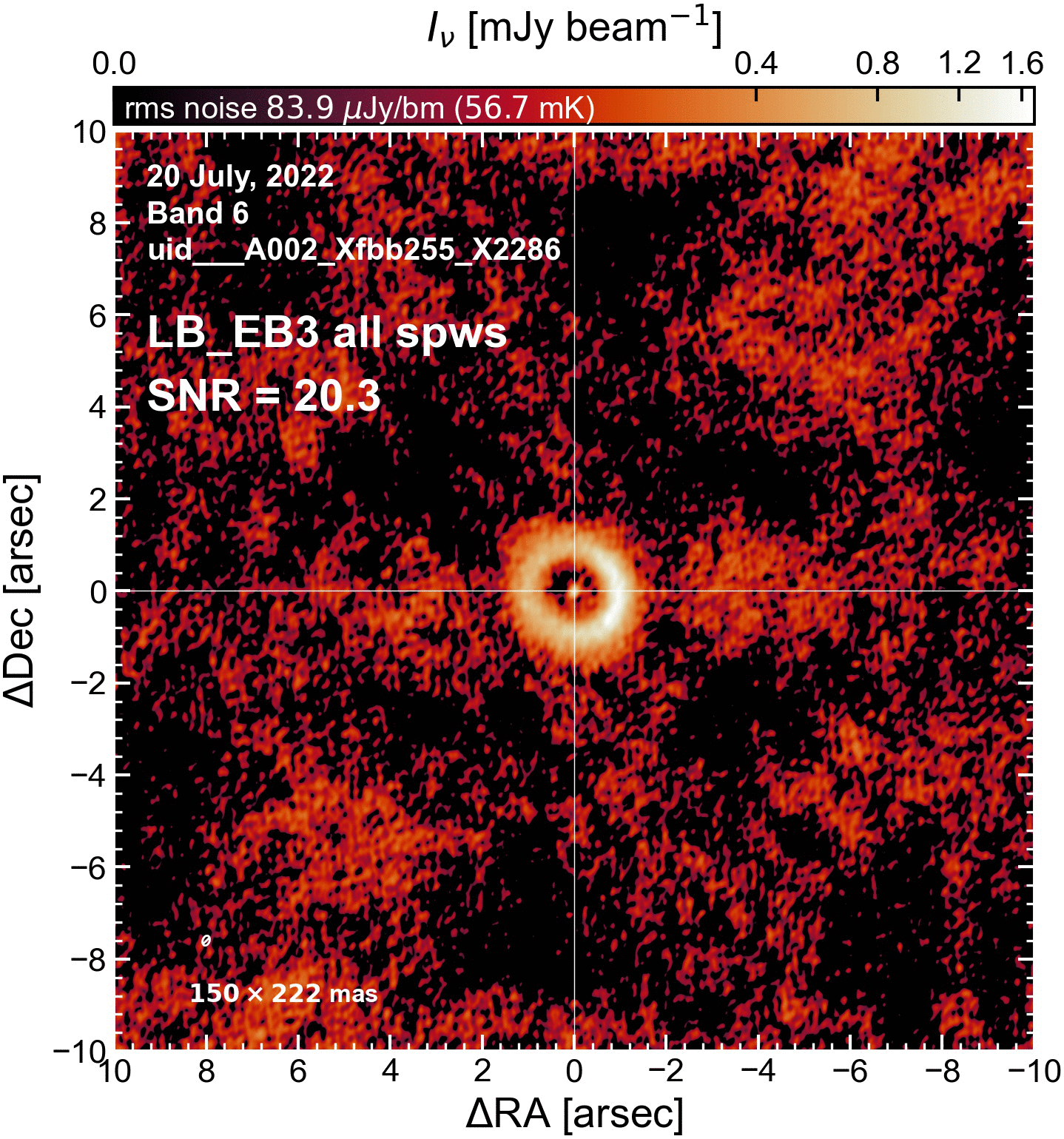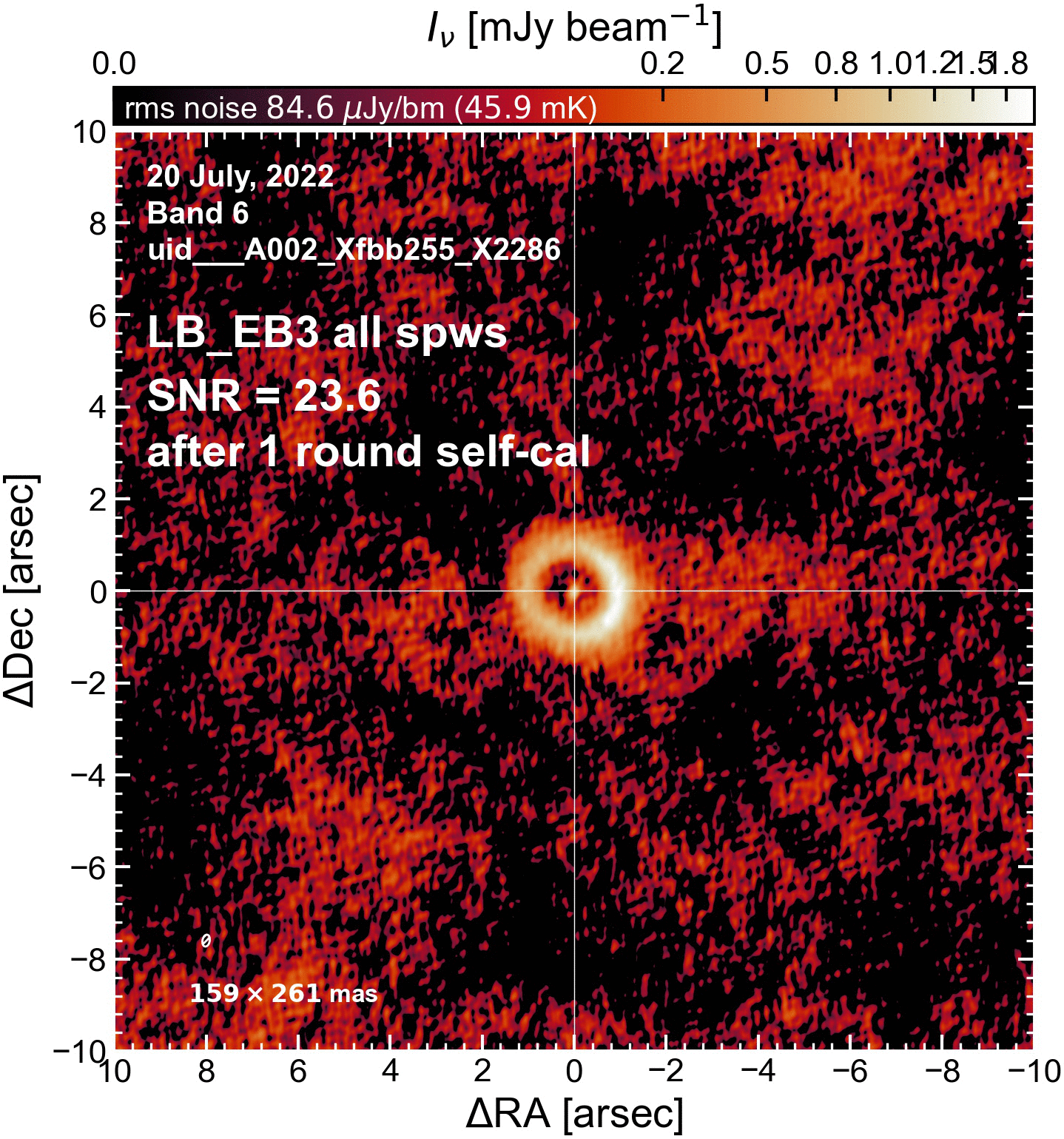
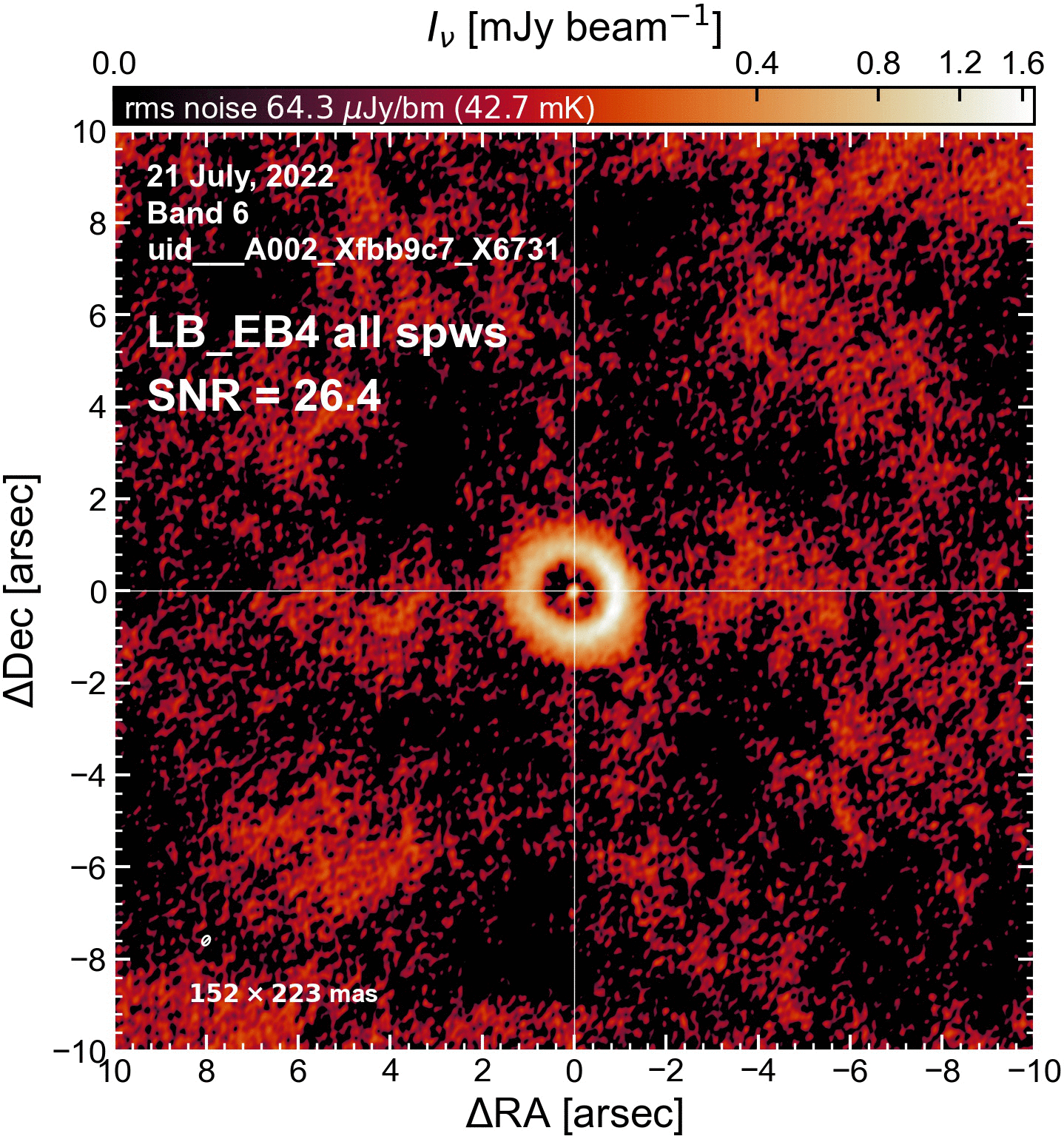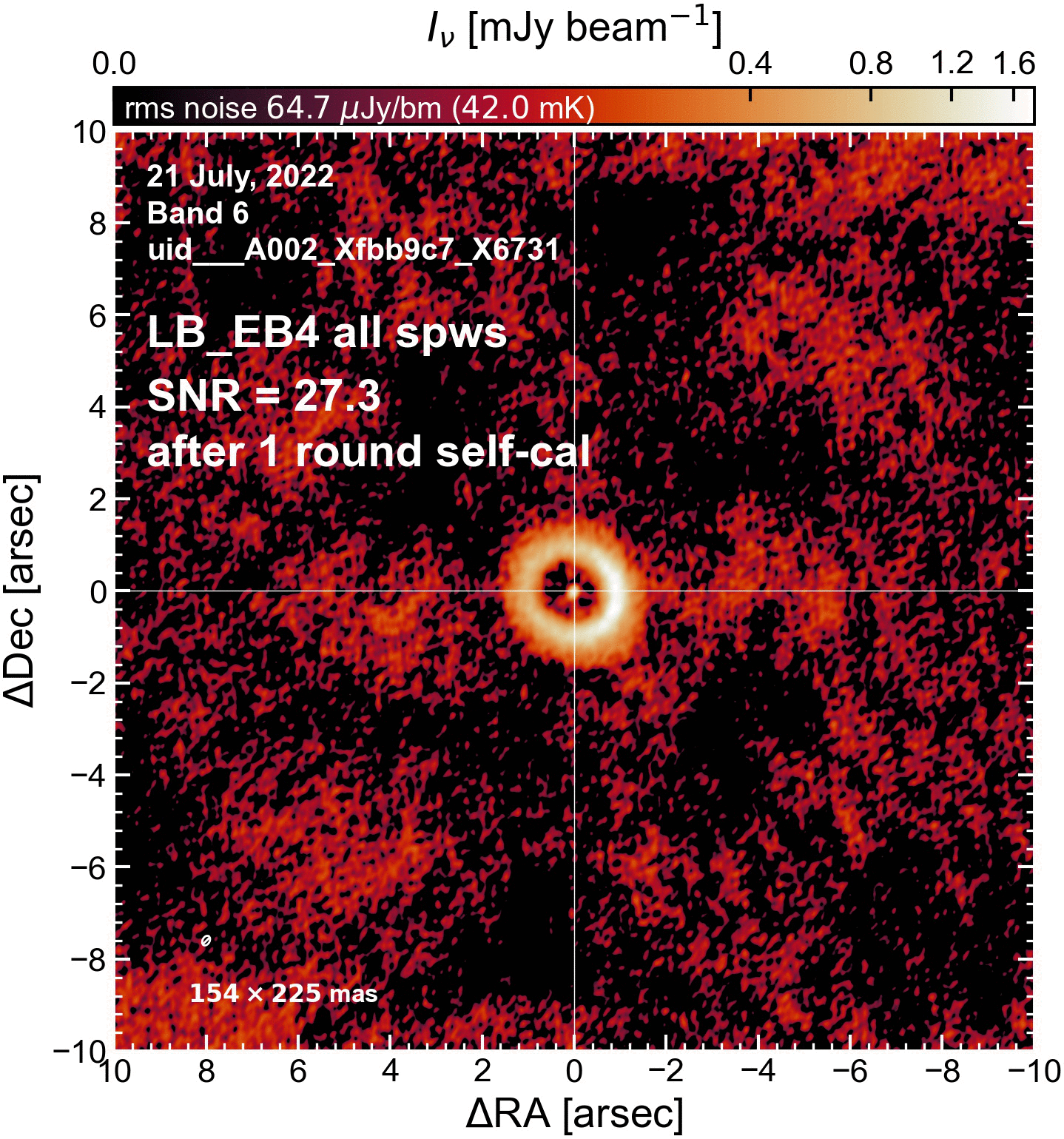
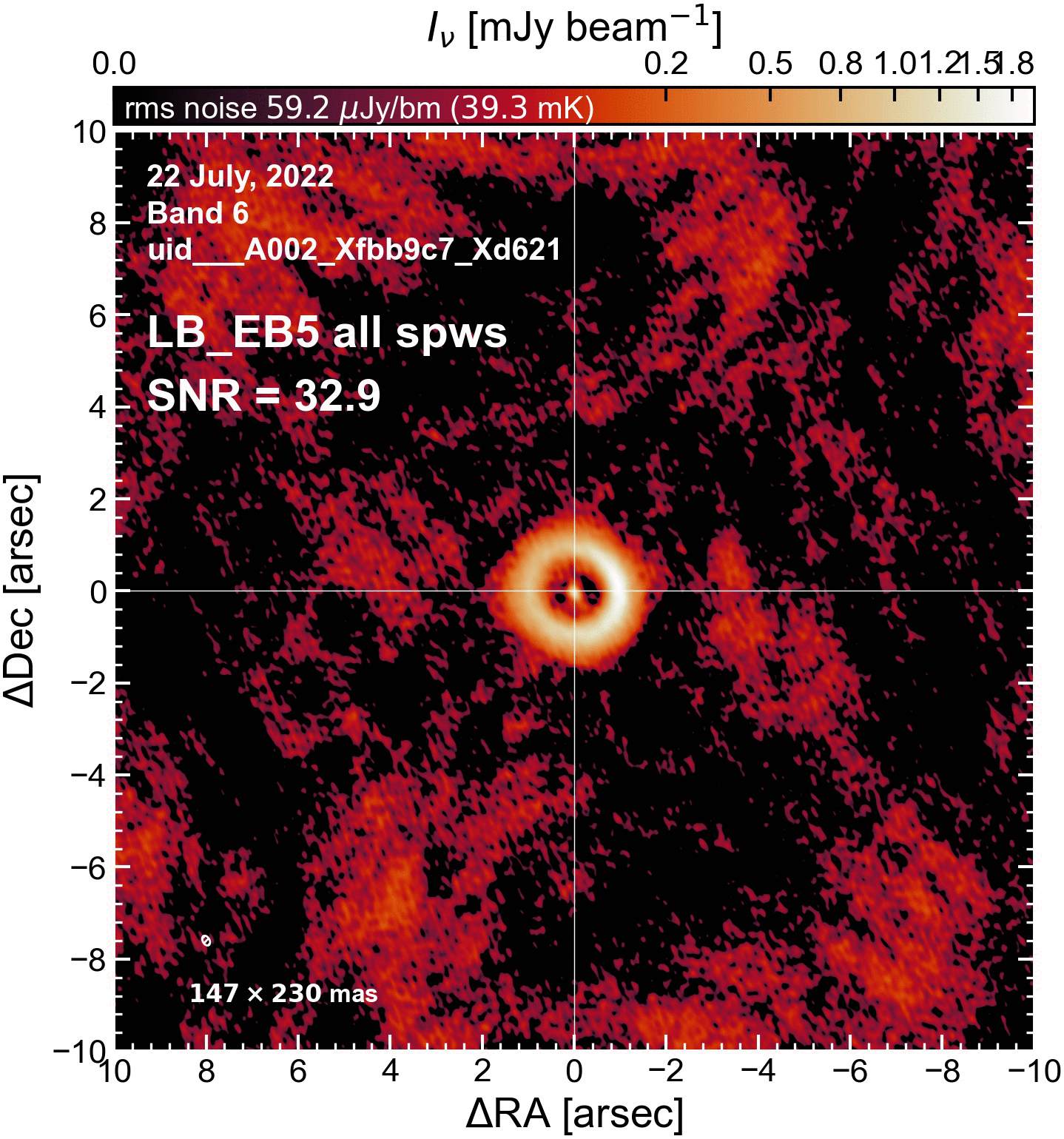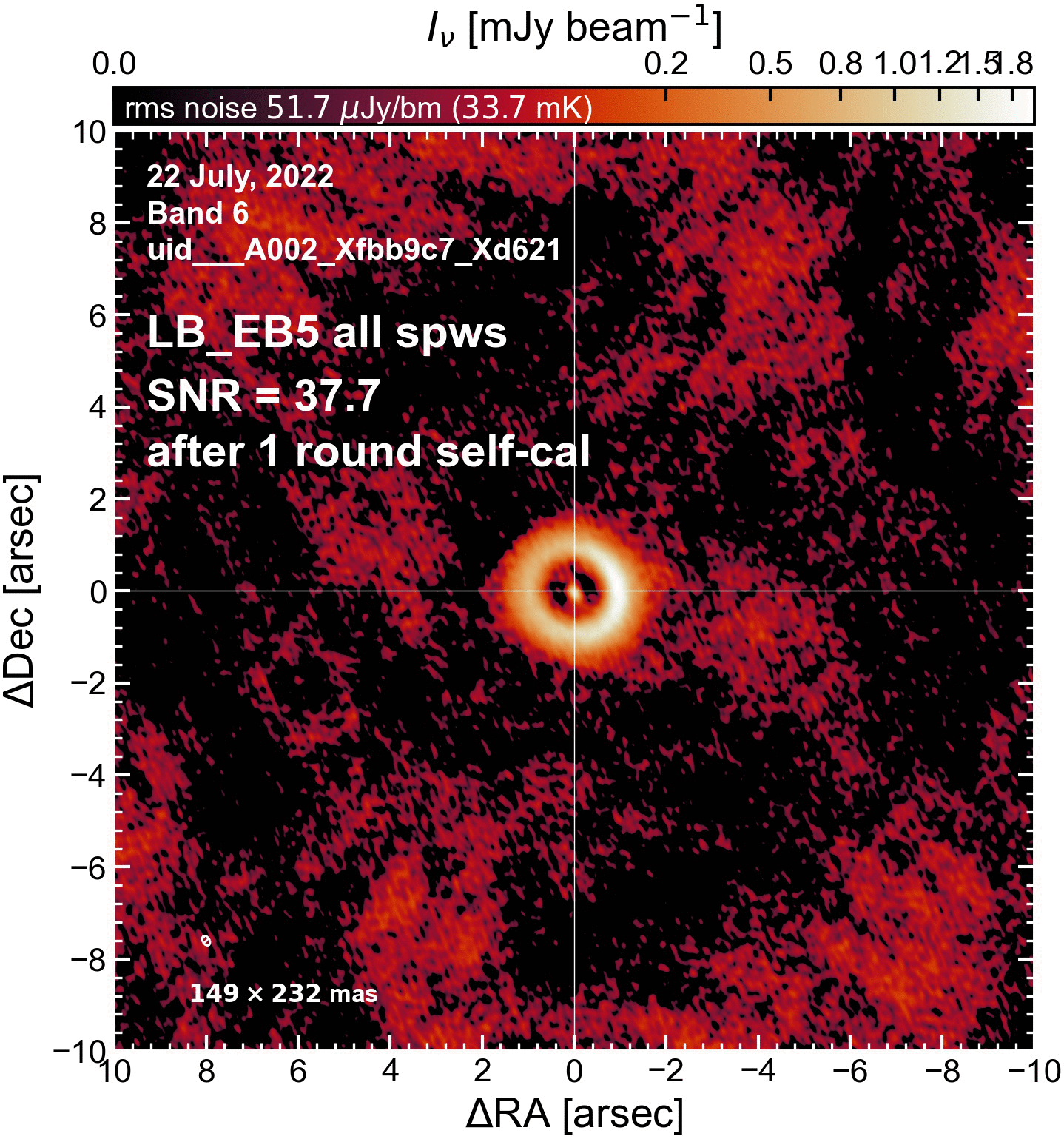
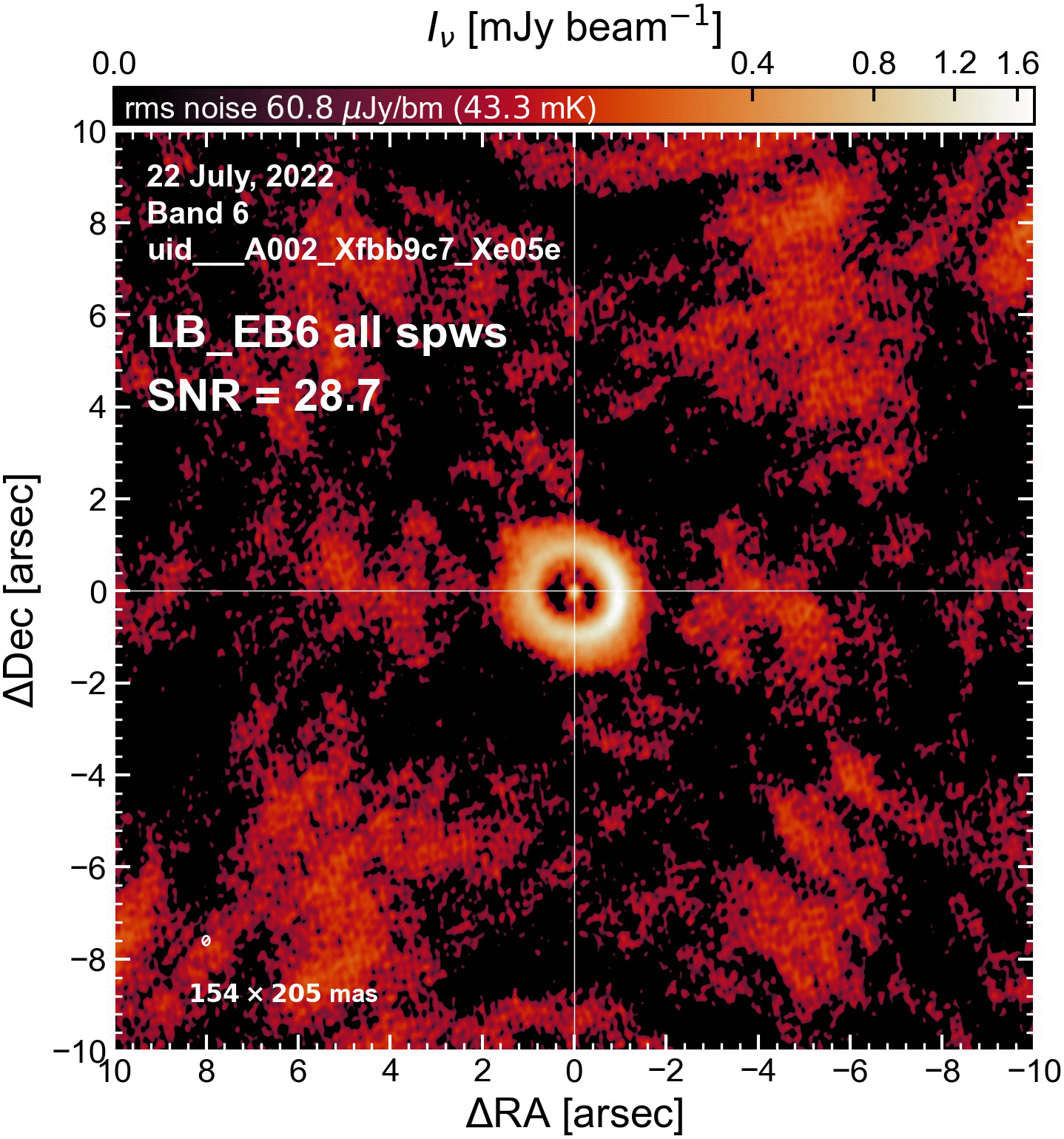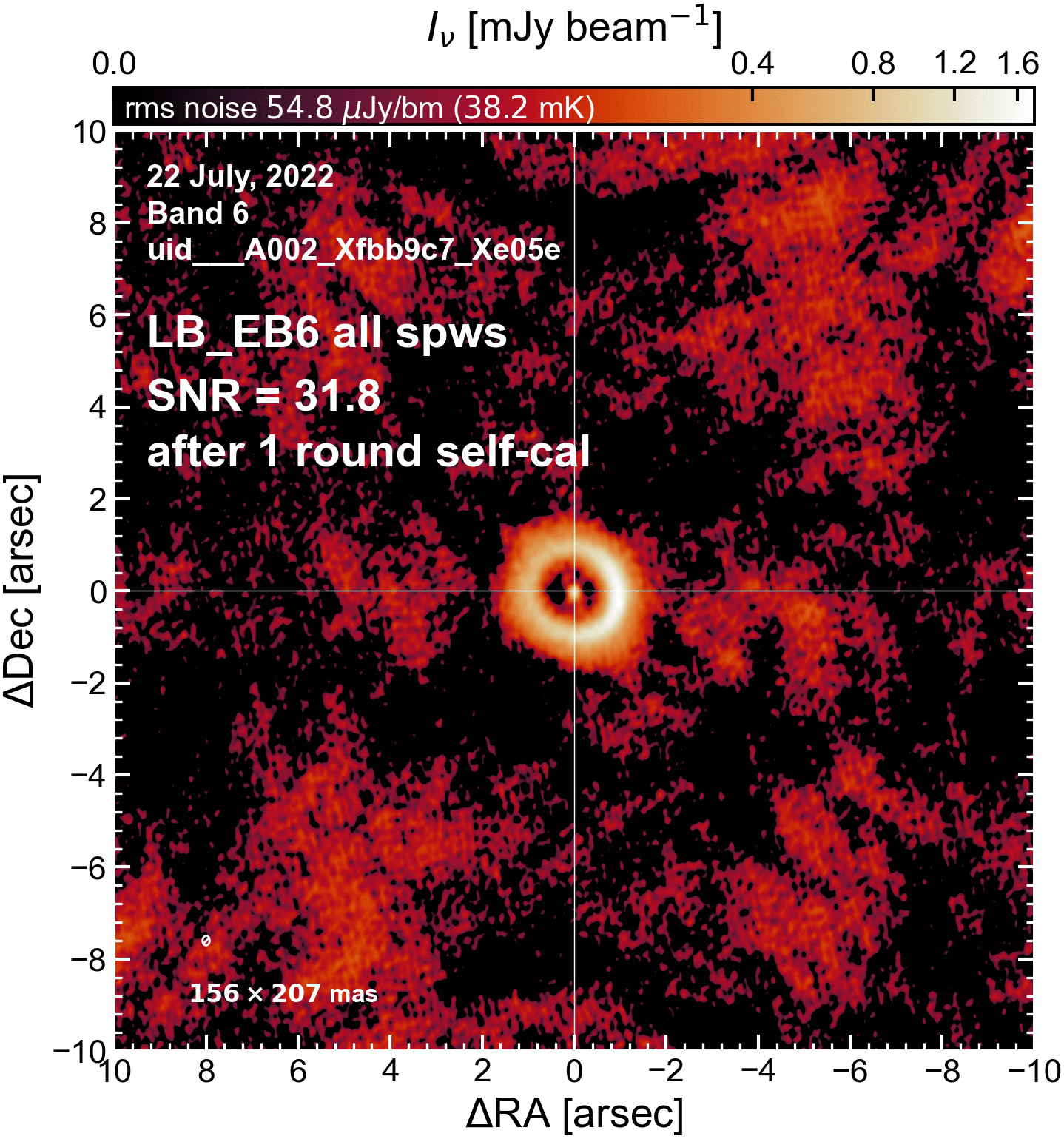
The results of this initial round of per-EB self-cal#

The SNR increased in all cases (some more than others).

SB EBs#

SB_EB1_model_selfcal SB_EB2_model_selfcal

Left to right: SB EB1, SB EB2.

LB EBs#

LB_EB1_model_selfcal LB_EB2_model_selfcal LB_EB3_model_selfcal LB_EB4_model_selfcal LB_EB5_model_selfcal LB_EB6_model_selfcal

Left to right, top to bottom: LB EB1, LB EB2, LB EB3, LB EB4, LB EB5, LB EB6.

Keeping track of results with selfcal_dict.txt

The function update_selfcal_dict in selfcal_utils.py helps to keep track of certain quantities that change as a result of self-calibration, such as the synthesized beam (which gets bigger if low SNR data is flagged by gaincal/applycal) and image properties (disk flux, SNR, etc). It’s used in step1_prepare_continuum.py on the initial model to establish the starting point before any self-cal:

update_selfcal_dict(selfcal_dict  = selfcal_dict,
                    round         = 'starting_model',
                    EB            = EB,
                    image_metrics = image_metrics)

And then again after this initial round of self-cal:

update_selfcal_dict(selfcal_dict  = selfcal_dict,
                    round         = 'initial_round',
                    EB            = EB,
                    image_metrics = image_metrics)

Here is the content of the resulting selfcal_dict.txt file:

{
"starting_model":
  {
    "SB_EB1": {"beammajor": 0.98555845022208, "beamminor": 0.6502565145492001, "beampa": -3.267037153244, "disk_flux": 96.37119767635464, "peak_intensity": 15.64478687942028, "rms": 110.25500110126073, "SNR": 141.89639221037916},
    "SB_EB2": {"beammajor": 0.84730178117736, "beamminor": 0.55687248706824, "beampa": -11.97756671906, "disk_flux": 92.91614621722621, "peak_intensity": 10.486830025911331, "rms": 111.60027276620909, "SNR": 93.96778131429969},
    "LB_EB1": {"beammajor": 0.25133076310158, "beamminor": 0.158669948577888, "beampa": -22.46494483948, "disk_flux": 102.21922520103227, "peak_intensity": 2.22735945135355, "rms": 59.83876249396578, "SNR": 37.22268573950138},
    "LB_EB2": {"beammajor": 0.2146227657795, "beamminor": 0.143906086683288, "beampa": 22.16491508484, "disk_flux": 64.31607986480157, "peak_intensity": 0.9940143208950758, "rms": 74.2708706723907, "SNR": 13.383636301770037},
    "LB_EB3": {"beammajor": 0.222091585397712, "beamminor": 0.15012736618518, "beampa": -20.48298072815, "disk_flux": 98.33766323017612, "peak_intensity": 1.7070583999156952, "rms": 85.4101918477119, "SNR": 19.986588988810784},
    "LB_EB4": {"beammajor": 0.222729876637452, "beamminor": 0.152399435639364, "beampa": -28.83377456665, "disk_flux": 94.4923150756974, "peak_intensity": 1.6992578748613596, "rms": 66.02184294954915, "SNR": 25.73781341062918},
    "LB_EB5": {"beammajor": 0.230228304862968, "beamminor": 0.14739404618739602, "beampa": 29.80331993103, "disk_flux": 103.8761273112917, "peak_intensity": 1.949697034433484, "rms": 58.18971866991047, "SNR": 33.505868029598496},
    "LB_EB6": {"beammajor": 0.204741835594164, "beamminor": 0.154411122202884, "beampa": -2.572570800781, "disk_flux": 95.24123482288928, "peak_intensity": 1.741013489663601, "rms": 59.81558891546768, "SNR": 29.106350388425138}
  }
"initial_round":
  {
    "SB_EB1": {"beammajor": 0.98555845022208, "beamminor": 0.6502565145492001, "beampa": -3.267035722733, "disk_flux": 97.37744327442131, "peak_intensity": 15.772012993693352, "rms": 81.13996805896602, "SNR": 194.38032046341846},
    "SB_EB2": {"beammajor": 0.8503259420393999, "beamminor": 0.55800050497056, "beampa": -12.06888866425, "disk_flux": 93.93793275833693, "peak_intensity": 10.558287613093853, "rms": 89.668852844978, "SNR": 117.747548653793},
    "LB_EB1": {"beammajor": 0.25463050603866, "beamminor": 0.160491451621068, "beampa": -22.56776428223, "disk_flux": 101.04137510466822, "peak_intensity": 2.245823619887233, "rms": 52.304309448011786, "SNR": 42.9376401980698},
    "LB_EB2": {"beammajor": 0.47473317384732, "beamminor": 0.206704244017584, "beampa": 25.47427558899, "disk_flux": 56.16015007566346, "peak_intensity": 2.806705655530095, "rms": 139.53317041782125, "SNR": 20.114970849767356},
    "LB_EB3": {"beammajor": 0.26145595312117204, "beamminor": 0.158696442842472, "beampa": -10.980427742, "disk_flux": 96.63220026886405, "peak_intensity": 1.9986922852694988, "rms": 86.05921215271813, "SNR": 23.22461750780008},
    "LB_EB4": {"beammajor": 0.22487176954746002, "beamminor": 0.15411971509455602, "beampa": -29.1448764801, "disk_flux": 96.10158140277751, "peak_intensity": 1.7663217149674892, "rms": 66.62911868938559, "SNR": 26.509756540557014},
    "LB_EB5": {"beammajor": 0.23194327950478802, "beamminor": 0.14885918796063602, "beampa": 29.62239074707, "disk_flux": 104.86656000266917, "peak_intensity": 1.9505757372826338, "rms": 50.55783934790038, "SNR": 38.581073923279504},
    "LB_EB6": {"beammajor": 0.207019567489608, "beamminor": 0.15601308643818, "beampa": -2.546737670898, "disk_flux": 95.5095751180149, "peak_intensity": 1.7425380647182465, "rms": 54.00177322236003, "SNR": 32.268163816456486}
  },
}